What is STRAIN
Before learning about strain gauges, learn what “strain” is first.
External force applied to an elastic material generates stress, which subsequently generates deformation of the material. At this time, the length L of the material extends to L+ΔL if applied force is a tensile force. The ratio of ΔL to L, that is ΔL/L, is called strain. (Precisely, this is called normal strain or longitudinal strain.) On the other hand, if compressive force is applied, the length L is reduced to L- ΔL. Strain at this time is (- ΔL)/L. Strain is usually represented as ε . Supposing the cross sectional area of the material to be A and the applied force to be P, stress σ will be P/A, since a stress is a force working on a definite cross sectional area. In a simple uniaxial stress field as illustrated below, strain ε is proportional to stress σ, thus an equation σ = E x ε is satisfied, provided that the stress σ does not exceed the elastic limit of the material. "E" in the equation is the elastic modulus (Young's modulus) of the material.
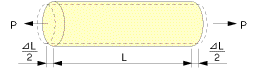
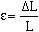 ε = ΔL/L
ε = ΔL/Lε : Strain
L : Original length
ΔL : Change due to force
Because a strain is a ratio between length of two parts, it is a quantity having no dimension. Usually it is represented in a unit of 1 x 10-6, since the ratio of deformation is often very small. For example, supposing L to be 100mm and ΔL to be 0.1mm, strain ε is indicated as 1000 x 10-6 strain, because "0.1mm/100mm=0.001=1 x 10-3=1000 x 10-6". To indicate comparatively large strain, "% strain" is also used. In this case, 1% strain equals to 10000 x 10-6 strain.
So strain is a very small value.
What is STRAIN GAUGE
Strain changes in only very minute values, so how is this measured with a strain gauge?
External force applied to a metallic material generates physical deformation and electrical resistance change of the material. In case that such material is sticked onto test specimen via electrical insulation, the material produces a change of electrical resistance corresponding to the deformation. Strain gauges consist of electrical resistance material and measure strains proportional to the resistance changes.

STRAIN GAUGE CONFIGURATION
In order to measure change in the resistance value due to extension of metal (resistor), how is a strain gauge structured?
A strain gauge is constructed by forming a grid made of fine electric resistance wire or photographically etched metallic resistance foil on an electrical insulation base (backing), and attaching gauge leads.
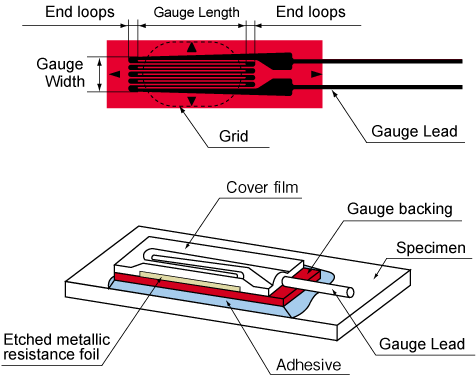
STRAIN GAUGE PRINCIPLES
We have seen how a strain gauge is structured. Next the principle of how strain is measured based on change in a resistance value due to extension of metal (resistor) will be explained.
When strain is generated in a test specimen and a strain gauge is atstached, the strain is relayed via the gauge base(electrical insulation) to the resistance wire or foil in the gauge. As a result, the fine wire or foil experiences a variation in electrical resistance. This variation is exactly proportional to the strain.

Normally, this resistance change is very small and requires a Wheatstone bridge circuit to convert the small resistance change to a more easily measured voltage change.

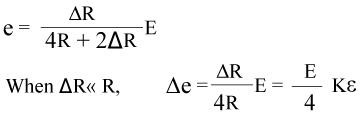
The voltage output of the circuit is given as follows.
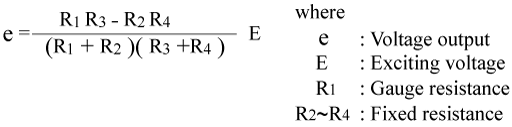
Here, if R=R1=R2=R3=R4 the resistance of the strain gauge changes to R+ΔR due to strain. Thus, the output voltage Δe (variation) due to the strain is given as follows.
When measuring with a strain gauge, it is connected to an instrument called a strainmeter. The strainmeter configures a Wheatstone bridge circuit and supplies exciting voltage. Measured strain is indicated on a digital display and/or output as analog signals.
SELECTING STRAIN GAUGES
Strain gauges are provided with many convenient features, but they also have limitations. Each strain gauge has its limitations in terms of temperature, fatigue, the amount of strain, and the measurement environment. These limitations must be examined before a strain gauge is used.

Strain Gauge Features
- Simple construction with a small mass and volume so as not to interfere with the stresses on the specimen.
- Short distance between measuring points for localized evaluation.
- Good frequency response for tracking rapid fluctuations in stress.
- Simultaneous measurement of multiple points and remote measurement.
- Electrical output for easy data processing.
More Information


